
四校联考2017—2018学年度第一学期期中考试
#高一物理试卷
#考试时间: 60分钟 总分: 100分
#一.单项选择题(本大题共20小题,每小题3分,共60分)
#请阅读下列材料,回答1 – 3 小题
#在冬季的时候,由于路面结冰,极易造成交通事故。一辆质量为3t的汽车,以40km/h的速度沿平直公路行驶,已知橡胶轮胎与普通路面的动摩擦因数为μ1 = 0.6,与结冰地面的动摩擦因数为μ2 = 0.2(g = 10m/s2)
#1.汽车的重力为
#A.3×102N B.3×103N C.3×104N D.3×105N
#2.在汽车正常行驶时,以汽车为参考系
#A.路边的树是静止的
#B.路边的树向后运动
#C.汽车里的乘客是运动的
#D.前方的汽车一定是运动的
#3.甲、乙两辆相同的汽车分别在普通路面和结冰地面上,刹车滑行做匀减速直线运动。下图中x表示位移、v表示速度,能正确描述该过程的图像是
#
#
#
#
4.在考察下列运动员的比赛成绩时,可视为质点的是
#A.马拉松 B.跳水 C.击剑 D.体操
#5.在运动会上,甲、乙两位同学进行百米赛跑,假如起跑加速的时间忽略,把他 们的运动近似当作匀速直线运动来处理.他们同时从起跑线起跑,经过一段时间后他们的位置如图所示,分别作出在这段时间内两人运动的位移x、速度v与时间t的关系图象如下,其中能正确反映他们运动的是
们的运动近似当作匀速直线运动来处理.他们同时从起跑线起跑,经过一段时间后他们的位置如图所示,分别作出在这段时间内两人运动的位移x、速度v与时间t的关系图象如下,其中能正确反映他们运动的是
#
#
#
6.下列物理量属于标量的是
#A.速度 B.位移 C.加速度 D.质量
# """ # path = r"F:\zwj\parse_2021\res_folder\13.html" # html = open(path,"r",encoding="utf-8").read() # # res = requests.post(url="http://192.168.1.140:11066/word_structure", json={"sci_html_data": html}) # print(res.text) # # 发送 # requests.get(url,params=data) # requests.post(url,files=files) # requests.post(url,data=data) # 接收get # request.args.get("user", "") 获取get请求参数 # request.values.get("key") 获取所有参数(POST\GET通用) # 接收post # request.form.get() 获取表单数据 # request.json.get() # request.files.get() # 如果请求体的数据不是表单格式的(如json格式,xml格式),可以通过request.data获取 # print(request.data) # {"name": "zhangsan", "age": 18} # args是用来提取url中?后拼接的参数(查询字符串QueryString) # city = request.args.get("city") # 127.0.0.1:5000/index?city=shenzhen (类似字典的对象) # request的属性为data、form、args、cookies、headers、method、url、files import json # import random # ft_modify = str(random.random()) # print(ft_modify) # # # resp = requests.post(url="http://192.168.1.145:10811/latex2img", data={"latex": "{ a > b {甲} }", "subfolder": "physical_formulas_imgs"}).text # print(resp) # bs = BeautifulSoup(html, 'lxml') # print(bs.prettify()) # tags = bs.find(name='script') # print(bs.script.string) # log_dir = r"C:\Users\Python\Desktop\test"+ r"\5fc0a554e3e93cca5b9e2193" # if not os.path.exists(log_dir): # os.mkdir(log_dir) # aa = ".wmf" # print(not aa.endswith(".wmf")) # print("AKIDC9pETRbZfWBbmhoglkT4PUJGzRjmj3Ia"=="AKIDC9pETRbZfWBbmhoglkT4PUJGzRjmj3Ia") # print("C6jlX4LKfleGdmfQvGNgj74lESRpBIEJ"=="C6jlX4LKfleGdmfQvGNgj74lESRpBIEJ") # from utils.ruku_opera import ruku_upload_img # # data_dir = "F:/zwj/Text_Structure/img_folder/struct_items.pickle" # html_dir = "F:/zwj/Text_Structure/img_folder/html_data.pickle" # items_list = pickle.load(open(data_dir, 'rb')) # html_data = pickle.load(open(html_dir, 'rb')) # wordid = "5fc64a0a4994183dda7e74b9" # res = ruku_upload_img(items_list, html_data, str(wordid)) # print(res) # qq=r' '
# new_imgs = re.findall(r'
'
# new_imgs = re.findall(r'14[答案] A [解析] 考查运动的合成与分解知识,橡皮参与两个分运动,即水平方向的匀速运动和竖直方向的匀速运动,故橡皮运动速度的大小" # a=re.sub(r"
\s*([1-9]|[1-4][0-9])\s*(【(解析?|答案?)】|(解析?|答案?)\s*[::]|\[(答案|解析)\])", r"
\1、\2", html2txt)
#
# print(a)
from structure.danti_structure import single_parse
s = '\\u2000'
s = s.encode('ascii', 'ignore').decode('ascii')
print(s)
LATEX_SYMS = ['\\leftrightharpoondowndown', '\\barleftarrowrightarrowba', '\\shortrightarrowleftarrow', '\\leftarrowshortrightarrow', '\\rightarrowshortleftarrow', '\\concavediamondtickright', '\\smallblacktriangleright', '\\updownharpoonrightright', '\\downupharpoonsleftright', '\\updownharpoonsleftright', '\\invwhitelowerhalfcircle', '\\nvtwoheadrightarrowtail', '\\invwhiteupperhalfcircle', '\\smallblacktriangleleft', '\\updownharpoonleftright', '\\downtrianglerightblack', '\\leftrightarrowtriangle', '\\blackcircleulquadwhite', '\\nvtwoheadleftarrowtail', '\\leftrightharpoondownup', '\\leftrightharpoonupdown', '\\concavediamondtickleft', '\\partialmeetcontraction', '\\updownharpoonrightleft', '\\downharpoonsleftright', '\\leftrightharpoonsdown', '\\circlebottomhalfblack', '\\closedvarcupsmashprod', '\\underrightharpoondown', '\\barovernorthwestarrow', '\\twoheadrightarrowtail', '\\blackdiamonddownarrow', '\\rightleftharpoonsdown', '\\updownharpoonleftleft', '\\downtriangleleftblack', '\\rangledownzigzagarrow', '\\whiteinwhitetriangle', '\\leftrightarrowcircle', '\\CapitalDifferentialD', '\\curvearrowrightminus', '\\bigblacktriangledown', '\\dashrightharpoondown', '\\barrightarrowdiamond', '\\leftrightharpoondown', '\\underleftharpoondown', '\\rightarrowbackapprox', '\\twoheaduparrowcircle', '\\whitesquaretickright', '\\blackrighthalfcircle', '\\twoheadleftarrowtail', '\\blackcircledownarrow', '\\blackcircledrightdot', '\\leftrightharpoonupup', '\\NestedGreaterGreater', '\\downrightcurvedarrow', '\\circlerighthalfblack', '\\rightdowncurvedarrow', '\\nvtwoheadrightarrow', '\\leftrightharpoonsup', '\\downharpoonrightbar', '\\leftrightsquigarrow', '\\twoheadleftdbkarrow', '\\blockthreeqtrshaded', '\\mbfitsansvarepsilon', '\\dashleftharpoondown', '\\upharpoonsleftright', '\\longrightsquigarrow', '\\rightleftharpoonsup', '\\whitearrowupfrombar', '\\whitesquaretickleft', '\\diamondleftarrowbar', '\\blackcircledtwodots', '\\bardownharpoonright', '\\leftdowncurvedarrow', '\\circlelefthalfblack', '\\blackinwhitediamond', '\\rightharpoonsupdown', '\\leftarrowbackapprox', '\\rightharpoondownbar', '\\blacklefthalfcircle', '\\barrightharpoondown', '\\rightarrowbsimilar', '\\longleftrightarrow', '\\blackinwhitesquare', '\\circledwhitebullet', '\\smalltriangleright', '\\nvtwoheadleftarrow', '\\barleftharpoondown', '\\rightarrowtriangle', '\\leftrightharpoonup', '\\PrecedesSlantEqual', '\\longleftsquigarrow', '\\overleftrightarrow', '\\upharpoonrightdown', '\\curvearrowleftplus', '\\acwopencirclearrow', '\\DownRightTeeVector', '\\rightharpoonaccent', '\\measuredrightangle', '\\leftharpoondownbar', '\\leftharpoonsupdown', '\\RightDownVectorBar', '\\blacktriangleright', '\\circleonrightarrow', '\\parallelogramblack', '\\trianglerightblack', '\\RightDownTeeVector', '\\rightrightharpoons', '\\bsimilarrightarrow', '\\DownRightVectorBar', '\\rightpentagonblack', '\\rightupdownharpoon', '\\circletophalfblack', '\\ccwundercurvearrow', '\\SucceedsSlantEqual', '\\downharpoonleftbar', '\\bigblacktriangleup', '\\Longleftrightarrow', '\\inversewhitecircle', '\\errbarblackdiamond', '\\rightharpoonupdash', '\\bardownharpoonleft', '\\smalltriangledown', '\\varhexagonlrbonds', '\\circleonleftarrow', '\\leftharpoonaccent', '\\mbfitsansvartheta', '\\barupharpoonright', '\\measuredangleleft', '\\varcarriagereturn', '\\mbfitsansvarsigma', '\\rightarrowonoplus', '\\DownLeftTeeVector', '\\cwopencirclearrow', '\\mbfsansvarepsilon', '\\twoheadrightarrow', '\\rightleftharpoons', '\\bsimilarleftarrow', '\\triangleleftblack', '\\upharpoonrightbar', '\\LeftDownTeeVector', '\\vardoublebarwedge', '\\circleurquadblack', '\\blacktriangleleft', '\\kernelcontraction', '\\LeftDownVectorBar', '\\rightarrowsimilar', '\\blackpointerright', '\\rightarrowdiamond', '\\uprightcurvearrow', '\\leftarrowtriangle', '\\leftupdownharpoon', '\\cwundercurvearrow', '\\diamondrightblack', '\\mbfitsansvarkappa', '\\smalltriangleleft', '\\errbarblackcircle', '\\rightharpoonupbar', '\\barrightharpoonup', '\\errbarblacksquare', '\\blacktriangledown', '\\leftharpoonupdash', '\\DownLeftVectorBar', '\\whitepointerright', '\\upharpoonleftdown', '\\acwgapcirclearrow', '\\leftarrowbsimilar', '\\similarrightarrow', '\\leftrightharpoons', '\\mbfitsansomicron', '\\mbfitsansepsilon', '\\rightrightarrows', '\\nvrightarrowtail', '\\rightarrowsupset', '\\twoheadleftarrow', '\\leftarrowsimilar', '\\barleftharpoonup', '\\diamondleftarrow', '\\rightarrowapprox', '\\whitepointerleft', '\\mbfitsanspartial', '\\RightUpTeeVector', '\\downdownharpoons', '\\ointctrclockwise', '\\acwunderarcarrow', '\\RightTriangleBar', '\\blackpointerleft', '\\RightUpVectorBar', '\\leftrightharpoon', '\\squarerightblack', '\\upharpoonleftbar', '\\NotRightTriangle', '\\downarrowuparrow', '\\vartriangleright', '\\sphericalangleup', '\\leftharpoonupbar', '\\diamondleftblack', '\\leftleftharpoons', '\\rightharpoondown', '\\APLrightarrowbox', '\\rightcurvedarrow', '\\similarleftarrow', '\\varointclockwise', '\\upharpoonrightup', '\\twoheaddownarrow', '\\uparrowdownarrow', '\\ntrianglerighteq', '\\mbfitsansupsilon', '\\nvleftrightarrow', '\\leftarrowonoplus', '\\barupharpoonleft', '\\uprevequilibrium', '\\rightleftharpoon', '\\downharpoonright', '\\rightthreearrows', '\\circlearrowright', '\\cwgapcirclearrow', '\\rightsquigarrow', '\\mbfitsansvarphi', '\\ntrianglelefteq', '\\underrightarrow', '\\unicodeellipsis', '\\leftharpoondown', '\\ulblacktriangle', '\\diamondbotblack', '\\urblacktriangle', '\\leftthreearrows', '\\downzigzagarrow', '\\vrectangleblack', '\\LeftUpTeeVector', '\\lrblacktriangle', '\\APLleftarrowbox', '\\rightbarharpoon', '\\squarecrossfill', '\\blockhalfshaded', '\\vartriangleleft', '\\acwleftarcarrow', '\\mbfsansvartheta', '\\diamondtopblack', '\\measanglerdtose', '\\LeftUpVectorBar', '\\rightwhitearrow', '\\measangleultonw', '\\upharpoonleftup', '\\measangledltosw', '\\multimapdotboth', '\\blacktriangleup', '\\nvleftarrowtail', '\\varhexagonblack', '\\nleftrightarrow', '\\circlearrowleft', '\\rightthreetimes', '\\barrightharpoon', '\\LeftTriangleBar', '\\leftcurvedarrow', '\\measangleldtosw', '\\enleadertwodots', '\\cwrightarcarrow', '\\mbfitvarepsilon', '\\measanglerutone', '\\leftarrowapprox', '\\mbfitsanslambda', '\\mbfsansvarsigma', '\\measangleurtone', '\\twoheadmapsfrom', '\\squareleftblack', '\\APLdownarrowbox', '\\smalltriangleup', '\\hrectangleblack', '\\downharpoonleft', '\\measangledrtose', '\\APLnotbackslash', '\\enclosetriangle', '\\downarrowbarred', '\\circledownarrow', '\\llblacktriangle', '\\mbfitsansvarrho', '\\trianglerighteq', '\\mbfsansvarkappa', '\\rightleftarrows', '\\circledparallel', '\\bigtriangleleft', '\\leftrightarrows', '\\measanglelutonw', '\\leftarrowsubset', '\\equalrightarrow', '\\NotGreaterTilde', '\\bigtriangledown', '\\widebridgeabove', '\\circledrightdot', '\\acwoverarcarrow', '\\curvearrowright', '\\uparrowoncircle', '\\NotLeftTriangle', '\\leftwhitearrow', '\\mbfitsansdelta', '\\leftbarharpoon', '\\mbfitsanssigma', '\\trianglelefteq', '\\revequilibrium', '\\blockrighthalf', '\\squarebotblack', '\\lparenextender', '\\rbrackextender', '\\underleftarrow', '\\ocommatopright', '\\vardiamondsuit', '\\bigslopedwedge', '\\rightleftarrow', '\\mbfitsansnabla', '\\mdlgblkdiamond', '\\leftthreetimes', '\\rightdasharrow', '\\downupharpoons', '\\upharpoonright', '\\rightharpoonup', '\\rightwavearrow', '\\wedgedoublebar', '\\mbfsanspartial', '\\lbrackextender', '\\rightanglemdot', '\\rparenextender', '\\looparrowright', '\\hookrightarrow', '\\leftrightarrow', '\\RightVectorBar', '\\equalleftarrow', '\\downwhitearrow', '\\mbfsansomicron', '\\circlevertfill', '\\RightTeeVector', '\\acwcirclearrow', '\\mdlgblklozenge', '\\downdownarrows', '\\Longrightarrow', '\\longmappedfrom', '\\mdlgwhtdiamond', '\\Longmappedfrom', '\\blackhourglass', '\\blockqtrshaded', '\\triangleserifs', '\\rightarrowplus', '\\mbfitsansvarpi', '\\longrightarrow', '\\enclosediamond', '\\mbfitsansomega', '\\sphericalangle', '\\leftsquigarrow', '\\updownharpoons', '\\mbfsansepsilon', '\\fdiagovnearrow', '\\overrightarrow', '\\NestedLessLess', '\\concavediamond', '\\mbfitsanskappa', '\\squareneswfill', '\\updownarrowbar', '\\rightarrowtail', '\\leftleftarrows', '\\mbfitsanstheta', '\\doublebarwedge', '\\carriagereturn', '\\NotGreaterLess', '\\mbfsansupsilon', '\\ntriangleright', '\\mbfitsansgamma', '\\squaretopblack', '\\rightouterjoin', '\\circledtwodots', '\\vbraceextender', '\\APLboxquestion', '\\curvearrowleft', '\\Leftrightarrow', '\\twoheaduparrow', '\\barleftharpoon', '\\rdiagovsearrow', '\\squarenwsefill', '\\harrowextender', '\\dashrightarrow', '\\mdlgwhtlozenge', '\\mbfitsansalpha', '\\mdlgblkcircle', '\\blocklefthalf', '\\bigtalloblong', '\\rightfishtail', '\\ntriangleleft', '\\bdtriplevdash', '\\mbfsansvarrho', '\\triangleminus', '\\mbfsansvarphi', '\\longleftarrow', '\\biginterleave', '\\parallelogram', '\\mdsmblkcircle', '\\mbfitvarsigma', '\\rightpentagon', '\\leftarrowplus', '\\SucceedsTilde', '\\mbfitsanszeta', '\\botsemicircle', '\\vysmblkcircle', '\\equalparallel', '\\mdlgwhtcircle', '\\PrecedesTilde', '\\Hermaphrodite', '\\circledbslash', '\\squarelrblack', '\\dashleftarrow', '\\mdsmblksquare', '\\rightarrowgtr', '\\triangletimes', '\\LeftTeeVector', '\\rightarrowbar', '\\llparenthesis', '\\mbfvarepsilon', '\\shortlefttack', '\\emptysetoarrl', '\\varlrtriangle', '\\smallsetminus', '\\vysmblksquare', '\\threedotcolon', '\\wasytherefore', '\\blacktriangle', '\\vysmwhtcircle', '\\threeunderdot', '\\leftwavearrow', '\\mdlgblksquare', '\\divideontimes', '\\leftdasharrow', '\\mbfitsansiota', '\\vysmwhtsquare', '\\varsubsetneqq', '\\mbfitvartheta', '\\leftouterjoin', '\\fallingdotseq', '\\enclosesquare', '\\dotsminusdots', '\\draftingarrow', '\\shortdowntack', '\\Longleftarrow', '\\APLboxupcaret', '\\overleftarrow', '\\LeftVectorBar', '\\twoheadmapsto', '\\downdasharrow', '\\circledbullet', '\\upequilibrium', '\\emptysetocirc', '\\leftharpoonup', '\\mbfitsansbeta', '\\RightArrowBar', '\\upharpoonleft', '\\uparrowbarred', '\\mdlgwhtsquare', '\\upbackepsilon', '\\squareulblack', '\\DifferentialD', '\\errbardiamond', '\\enclosecircle', '\\wideangledown', '\\APLuparrowbox', '\\mbfsanslambda', '\\leftarrowtail', '\\mitvarepsilon', '\\inversebullet', '\\squarellblack', '\\mdsmwhtsquare', '\\rrparenthesis', '\\fullouterjoin', '\\triangleright', '\\mbfitvarkappa', '\\cwcirclearrow', '\\measuredangle', '\\mdsmwhtcircle', '\\hookleftarrow', '\\rightanglesqr', '\\pentagonblack', '\\looparrowleft', '\\bigtriangleup', '\\rightdotarrow', '\\leftarrowless', '\\squareurblack', '\\sixteenthnote', '\\topsemicircle', '\\RightTriangle', '\\mbfsansthree', '\\mbfitsansphi', '\\hexagonblack', '\\doublebarvee', '\\LeftTriangle', '\\squareulquad', '\\varsubsetneq', '\\triangleplus', '\\unicodecdots', '\\Longmapsfrom', '\\upvarepsilon', '\\ogreaterthan', '\\squareurquad', '\\leftdbkarrow', '\\mdblkdiamond', '\\squarehvfill', '\\NotLessTilde', '\\downarrowbar', '\\closedvarcap', '\\DownArrowBar', '\\barleftarrow', '\\longmapsfrom', '\\mbfitsanschi', '\\mbfsansgamma', '\\upwhitearrow', '\\varepsilonup', '\\mdwhtlozenge', '\\smwhtdiamond', '\\downfishtail', '\\dottedcircle', '\\wedgemidvert', '\\lozengeminus', '\\mbfsansdelta', '\\bigwhitestar', '\\mathsterling', '\\veedoublebar', '\\mbfitpartial', '\\mdblklozenge', '\\varspadesuit', '\\odotslashdot', '\\mbfsansalpha', '\\circledequal', '\\mbfitsanstau', '\\medblackstar', '\\cupleftarrow', '\\circlellquad', '\\rbracklrtick', '\\dottedsquare', '\\npreccurlyeq', '\\mbfitepsilon', '\\mbfsanskappa', '\\circleulquad', '\\lrtriangleeq', '\\squarellquad', '\\circlelrquad', '\\blacklozenge', '\\eqqslantless', '\\nsucccurlyeq', '\\mbfitupsilon', '\\notbackslash', '\\mbfsansseven', '\\blocklowhalf', '\\errbarcircle', '\\mbfitsansvar', '\\mbfitsanspsi', '\\smwhtlozenge', '\\rdiagovfdiag', '\\smblklozenge', '\\mdwhtdiamond', '\\lbracklltick', '\\PropertyLine', '\\medwhitestar', '\\revangleubar', '\\intclockwise', '\\risingdotseq', '\\longdivision', '\\LeftArrowBar', '\\varheartsuit', '\\triangleubar', '\\rbrackurtick', '\\leftfishtail', '\\multimapboth', '\\mbfsanstheta', '\\upupharpoons', '\\trianglecdot', '\\mbfitomicron', '\\fdiagovrdiag', '\\smblkdiamond', '\\lbrackultick', '\\invsmileface', '\\subsetapprox', '\\nvrightarrow', '\\triangledown', '\\mbfsanssigma', '\\hyphenbullet', '\\rightdbltail', '\\closedvarcup', '\\mbfsansvarpi', '\\errbarsquare', '\\Diamondblack', '\\leftdotarrow', '\\updownarrows', '\\wedgeonwedge', '\\squarelrquad', '\\bigslopedvee', '\\triangleleft', '\\triangleodot', '\\emptysetobar', '\\downuparrows', '\\rightbkarrow', '\\cntclockoint', '\\oturnedcomma', '\\circleurquad', '\\mbfitsansrho', '\\dingasterisk', '\\mbfsanseight', '\\hermitmatrix', '\\GreaterTilde', '\\supsetapprox', '\\mbfitsanseta', '\\mbfsansomega', '\\emptysetoarr', '\\underbracket', '\\mbfsansnabla', '\\sqsubsetneq', '\\circleddash', '\\mbfsansiota', '\\squarehfill', '\\corresponds', '\\approxident', '\\midbarwedge', '\\leftdbltail', '\\APLnotslash', '\\lgblksquare', '\\vertoverlay', '\\quarternote', '\\diamondcdot', '\\mbfsansfive', '\\mitvarsigma', '\\smwhtcircle', '\\circledless', '\\nvleftarrow', '\\mitvarkappa', '\\blacksquare', '\\blkvertoval', '\\ruledelayed', '\\circledvert', '\\succnapprox', '\\nwovnearrow', '\\otimesrhrim', '\\Rrightarrow', '\\mbfitsanspi', '\\RIGHTCIRCLE', '\\mbfvarsigma', '\\mbfitvarphi', '\\mdwhtsquare', '\\blacksmiley', '\\mbfsanszero', '\\curlyeqsucc', '\\mbfitsansnu', '\\neovsearrow', '\\smwhitestar', '\\whthorzoval', '\\mbfsansbeta', '\\wasylozenge', '\\mdwhtcircle', '\\mbfitsansxi', '\\wideangleup', '\\diamondsuit', '\\preccurlyeq', '\\mbfitlambda', '\\varclubsuit', '\\updownarrow', '\\lcurvyangle', '\\caretinsert', '\\smblksquare', '\\eqslantless', '\\varbarwedge', '\\capricornus', '\\smwhtsquare', '\\squarevfill', '\\mbfvartheta', '\\rightarrowx', '\\leftbkarrow', '\\vartriangle', '\\shortuptack', '\\backtrprime', '\\overbracket', '\\whtvertoval', '\\mbfitsansmu', '\\mitvartheta', '\\curlyeqprec', '\\smblkcircle', '\\restriction', '\\ballotcheck', '\\mbfsansfour', '\\seovnearrow', '\\nrightarrow', '\\asteraccent', '\\mbfvarkappa', '\\Planckconst', '\\succcurlyeq', '\\blkhorzoval', '\\RIGHTcircle', '\\mbfsansnine', '\\threedangle', '\\circledstar', '\\neovnwarrow', '\\blockuphalf', '\\multimapinv', '\\mdblksquare', '\\ExponetialE', '\\precnapprox', '\\sagittarius', '\\rcurvyangle', '\\nsqsubseteq', '\\lgwhtcircle', '\\lgblkcircle', '\\sqsupsetneq', '\\revemptyset', '\\equilibrium', '\\mbfitvarrho', '\\updasharrow', '\\circledcirc', '\\simminussim', '\\GreaterLess', '\\intextender', '\\mdblkcircle', '\\eqqslantgtr', '\\lgwhtsquare', '\\gleichstark', '\\backepsilon', '\\otimeslhrim', '\\mbfsanszeta', '\\Updownarrow', '\\RRightarrow', '\\nsqsupseteq', '\\varisinobar', '\\arrowbullet', '\\msansseven', '\\mbfitsansx', '\\eighthnote', '\\mbfitsansf', '\\mbfsanseta', '\\rparenlend', '\\minusrdots', '\\APLcomment', '\\mbfitsanss', '\\mbfdigamma', '\\gtreqqless', '\\plussubtwo', '\\lessapprox', '\\upoldkoppa', '\\lltriangle', '\\mitupsilon', '\\mbfittheta', '\\mbfitsansa', '\\baruparrow', '\\vrectangle', '\\varnothing', '\\mbfsanspsi', '\\mbfitsansl', '\\Diamonddot', '\\rparenuend', '\\mbfitsansq', '\\lblkbrbrak', '\\subsetcirc', '\\mbfsanstau', '\\supsetplus', '\\LEFTCIRCLE', '\\curlywedge', '\\rbracklend', '\\sqrtbottom', '\\mbfitsansw', '\\hrectangle', '\\backdprime', '\\mbfitsansp', '\\sqsupseteq', '\\mitpartial', '\\mbfsanstwo', '\\rbraceuend', '\\rblkbrbrak', '\\mbfitsanst', '\\postalmark', '\\oplusrhrim', '\\eqslantgtr', '\\mbfitsanso', '\\mbfitsansy', '\\commaminus', '\\upfishtail', '\\interleave', '\\Rparenless', '\\rightangle', '\\tripleplus', '\\upvarkappa', '\\DDownarrow', '\\mathdollar', '\\msanseight', '\\pointright', '\\nleftarrow', '\\mbfitsansn', '\\varthetaup', '\\LEFTcircle', '\\varhexagon', '\\conictaper', '\\circledgtr', '\\upvartheta', '\\turnediota', '\\underparen', '\\mbfsansvar', '\\mbfitsansi', '\\smashtimes', '\\rightslice', '\\doubleplus', '\\Rightarrow', '\\mathsfbfit', '\\mbfitsansb', '\\circlehbar', '\\varsigmaup', '\\lparenless', '\\precapprox', '\\mbfitsansk', '\\mbfsanssix', '\\mbfitgamma', '\\mbfitvarpi', '\\subsetplus', '\\mbfitomega', '\\mbfitsansv', '\\mbfpartial', '\\varepsilon', '\\underbrace', '\\ultriangle', '\\msansthree', '\\supsetcirc', '\\vardiamond', '\\Lleftarrow', '\\mbfepsilon', '\\mbfitkappa', '\\talloblong', '\\circledast', '\\twolowline', '\\octothorpe', '\\Proportion', '\\cupovercap', '\\urtriangle', '\\rightarrow', '\\mbfitsansz', '\\lbracklend', '\\succapprox', '\\rightimply', '\\mbfitdelta', '\\mbfomicron', '\\lparenlend', '\\veeonwedge', '\\subsetneqq', '\\rbrackuend', '\\lbrackubar', '\\lparenuend', '\\longmapsto', '\\wideutilde', '\\fourthroot', '\\opluslhrim', '\\mbfitnabla', '\\rbrackubar', '\\mappedfrom', '\\mitomicron', '\\mitepsilon', '\\mbfupsilon', '\\lmoustache', '\\upuparrows', '\\lbraceuend', '\\mbfsansrho', '\\supsetneqq', '\\mbfitsansh', '\\rbracelend', '\\SetDelayed', '\\lbracelend', '\\mbfitsansj', '\\LLeftarrow', '\\lrtriangle', '\\Longmapsto', '\\mbfsansphi', '\\mbfitsansm', '\\mbfsansone', '\\sqsubseteq', '\\mbfitalpha', '\\mbfitsansc', '\\minusfdots', '\\leftarrowx', '\\upvarsigma', '\\mbfitsigma', '\\mbfitsansd', '\\mbfitsansr', '\\mbfitsansg', '\\veemidvert', '\\mbfitsanse', '\\mbfsanschi', '\\UpArrowBar', '\\complement', '\\capovercup', '\\rmoustache', '\\Ddownarrow', '\\mbfitsansu', '\\Mappedfrom', '\\lesseqqgtr', '\\Eulerconst', '\\lbrackuend', '\\CheckedBox', '\\mbfitsans', '\\msansnine', '\\Lparengtr', '\\dasharrow', '\\backslash', '\\mathcolon', '\\trapezium', '\\turnednot', '\\modtwosum', '\\bigcupdot', '\\capbarcup', '\\LessTilde', '\\varveebar', '\\ngeqslant', '\\llbracket', '\\supsetneq', '\\underline', '\\rvboxline', '\\gtrapprox', '\\righttail', '\\nsubseteq', '\\lvboxline', '\\downarrow', '\\Downarrow', '\\hknwarrow', '\\medbullet', '\\mathslash', '\\supseteqq', '\\tieconcat', '\\therefore', '\\mbfsansxi', '\\rangledot', '\\fracslash', '\\typecolon', '\\hatapprox', '\\Leftarrow', '\\triangles', '\\subseteqq', '\\sumbottom', '\\boxcircle', '\\leftarrow', '\\neswarrow', '\\msansfour', '\\upupsilon', '\\angleubar', '\\overbrace', '\\subsetneq', '\\mbfsansmu', '\\mbfsansnu', '\\intbottom', '\\biohazard', '\\epsilonup', '\\lbracemid', '\\turnangle', '\\approxeqq', '\\nleqslant', '\\mbfitiota', '\\leftslice', '\\mitlambda', '\\bagmember', '\\spadesuit', '\\conjquant', '\\semicolon', '\\wedgeodot', '\\rparengtr', '\\checkmark', '\\accurrent', '\\lesseqgtr', '\\triangleq', '\\mbflambda', '\\nparallel', '\\overparen', '\\mbfitzeta', '\\rightmoon', '\\midbarvee', '\\upsilonup', '\\wideparen', '\\msansfive', '\\radiation', '\\supsetdot', '\\geqqslant', '\\upepsilon', '\\rightturn', '\\backsimeq', '\\mitvarrho', '\\boxbslash', '\\vlongdash', '\\hknearrow', '\\dashcolon', '\\updigamma', '\\ampersand', '\\nsupseteq', '\\bigotimes', '\\varniobar', '\\pitchfork', '\\DashVDash', '\\increment', '\\nwsearrow', '\\mathratio', '\\subsetdot', '\\cupbarcap', '\\Angstroem', '\\impliedby', '\\leqqslant', '\\olessthan', '\\upvarbeta', '\\blockfull', '\\heartsuit', '\\upomicron', '\\hourglass', '\\mbfsanspi', '\\rrbracket', '\\partialup', '\\clockoint', '\\rbracemid', '\\mbfvarrho', '\\backprime', '\\mbfvarphi', '\\fourvdots', '\\mitvarphi', '\\gtreqless', '\\langledot', '\\otimeshat', '\\smileface', '\\longdashv', '\\disjquant', '\\mbfitbeta', '\\lightning', '\\msanszero', '\\sqlozenge', '\\mbffrakw', '\\mathbfit', '\\mitsansf', '\\mbffrakr', '\\clubsuit', '\\emptyset', '\\mbfsansg', '\\forksnot', '\\vartheta', '\\BbbGamma', '\\mitsansr', '\\msansone', '\\upvarrho', '\\mitvarpi', '\\Bbbthree', '\\mbffraku', '\\mitalpha', '\\mbfitrho', '\\mitsanse', '\\mbfsansd', '\\twonotes', '\\Bbbeight', '\\mbfsigma', '\\leftturn', '\\hksearow', '\\Rvzigzag', '\\mbffrakm', '\\ComplexJ', '\\smeparsl', '\\mbffrakq', '\\mbfalpha', '\\mitsansz', '\\mitsansk', '\\upvarphi', '\\mbffrakk', '\\mitsansj', '\\mitsansp', '\\approxeq', '\\subseteq', '\\sterling', '\\biguplus', '\\mapsdown', '\\astrosun', '\\hkswarow', '\\eqvparsl', '\\gesdotol', '\\mbfitvar', '\\lefttail', '\\lnapprox', '\\mitsanss', '\\varphiup', '\\profsurf', '\\mitsansh', '\\llcorner', '\\mathsfit', '\\sqsubset', '\\msanssix', '\\mbfdelta', '\\bigsqcup', '\\mitsansa', '\\mitsanst', '\\succnsim', '\\mbfsansp', '\\UUparrow', '\\gnapprox', '\\pullback', '\\mbfsanse', '\\underbar', '\\ComplexI', '\\bigwedge', '\\mittheta', '\\bbrktbrk', '\\mitsansd', '\\linefeed', '\\curlyvee', '\\notasymp', '\\supseteq', '\\mbfitchi', '\\mbfnabla', '\\backcong', '\\mitdelta', '\\mathbold', '\\invlazys', '\\triangle', '\\ulcorner', '\\mathfrak', '\\diameter', '\\lesdotor', '\\mbffrako', '\\Bbbseven', '\\mitsansn', '\\Mapsfrom', '\\mitsansu', '\\mbfsansh', '\\mathring', '\\zproject', '\\divslash', '\\varkappa', '\\mitgamma', '\\mbffrakh', '\\MapsDown', '\\cuberoot', '\\barwedge', '\\mbffrakl', '\\mbffrakf', '\\mbfsansj', '\\varrhoup', '\\mbfsansf', '\\precnsim', '\\mbffrakv', '\\mbfsansv', '\\varheart', '\\APLinput', '\\geqslant', '\\profline', '\\mbfsansl', '\\mbfvarpi', '\\coloneqq', '\\strictfi', '\\Bbbgamma', '\\mitnabla', '\\Question', '\\notowner', '\\bullseye', '\\mbfsansc', '\\varspade', '\\mbfgamma', '\\wedgebar', '\\Coloneqq', '\\precneqq', '\\mbffrakj', '\\mtteight', '\\medspace', '\\mbffraks', '\\mbffraki', '\\mbffraka', '\\doteqdot', '\\mbffrake', '\\strictif', '\\boxtimes', '\\mitsansl', '\\upstigma', '\\ringplus', '\\ngtrless', '\\lfbowtie', '\\horizbar', '\\mbfsansx', '\\mbfsansy', '\\mitkappa', '\\Uuparrow', '\\lambdaup', '\\mathsfbf', '\\veeonvee', '\\drbkarow', '\\mbffrakx', '\\plustrif', '\\dotequiv', '\\scpolint', '\\mbfsansk', '\\rtriltri', '\\mitsansv', '\\mitsansb', '\\rppolint', '\\mitsansx', '\\mitsanso', '\\simrdots', '\\dottimes', '\\smallint', '\\mbfsanss', '\\parallel', '\\capwedge', '\\mbfsanst', '\\mitsansi', '\\boxonbox', '\\mitsansq', '\\rfbowtie', '\\lrcorner', '\\mbffraky', '\\mbffrakc', '\\mitsansc', '\\boxminus', '\\mbfsansb', '\\elinters', '\\mbfsansi', '\\mbftheta', '\\mbfsansu', '\\viewdata', '\\bsolhsub', '\\timesbar', '\\msanstwo', '\\nlessgtr', '\\mbfitphi', '\\mbffrakn', '\\isinobar', '\\mathcent', '\\intlarhk', '\\mttseven', '\\mbfitpsi', '\\mitsansg', '\\mttthree', '\\mbfsansr', '\\pointint', '\\overline', '\\dotminus', '\\mbffrakb', '\\varsigma', '\\mbfkappa', '\\mbfiteta', '\\mbffrakd', '\\bigtimes', '\\mbfsanso', '\\acidfree', '\\mitsansy', '\\mbfittau', '\\mbfomega', '\\mbffrakz', '\\mbffrakp', '\\wedgedot', '\\mbfsansz', '\\intprodr', '\\mbfsansa', '\\uplambda', '\\mbfsansq', '\\mbffrakt', '\\sinewave', '\\nlesssim', '\\rvzigzag', '\\pentagon', '\\minusdot', '\\mbfsansm', '\\bigsqcap', '\\mapsfrom', '\\multimap', '\\lvzigzag', '\\intercal', '\\leqslant', '\\sqsupset', '\\vectimes', '\\boxslash', '\\mitsansw', '\\question', '\\notslash', '\\mbffrakg', '\\bigoplus', '\\mitomega', '\\cirfnint', '\\succneqq', '\\tieinfty', '\\steaming', '\\mbfsansn', '\\setminus', '\\Angstrom', '\\eqqcolon', '\\varisins', '\\revangle', '\\mitsigma', '\\Lvzigzag', '\\aquarius', '\\leftmoon', '\\dotequal', '\\mbfsansw', '\\mitsansm', '\\urcorner', '\\mttfour', '\\plushat', '\\epsilon', '\\trslash', '\\varbeta', '\\lesdoto', '\\simneqq', '\\gesdoto', '\\preceqq', '\\Swarrow', '\\mbfitxi', '\\boxdiag', '\\upkoppa', '\\varprod', '\\isindot', '\\mitiota', '\\npolint', '\\upsilon', '\\mitbeta', '\\supmult', '\\bigstar', '\\ballotx', '\\dualmap', '\\suphsub', '\\Digamma', '\\mitsans', '\\ggcurly', '\\circled', '\\uparrow', '\\matheth', '\\rbrbrak', '\\imageof', '\\plusdot', '\\bigodot', '\\congdot', '\\diamond', '\\fisheye', '\\Bbbnine', '\\eqcolon', '\\mbfitnu', '\\dbloint', '\\intprod', '\\upsigma', '\\npreceq', '\\mbfscrd', '\\Rbrbrak', '\\percent', '\\mbfscrs', '\\mbfscrn', '\\Scorpio', '\\mbfscrx', '\\mttnine', '\\uptheta', '\\searrow', '\\smallin', '\\upgamma', '\\lesssim', '\\rsqhook', '\\mbfscrl', '\\rsolbar', '\\hexagon', '\\medcirc', '\\obrbrak', '\\kappaup', '\\succsim', '\\lbrbrak', '\\topfork', '\\sadface', '\\gammaup', '\\omegaup', '\\lrtimes', '\\mbfscry', '\\digamma', '\\recycle', '\\ubrbrak', '\\nexists', '\\upvarpi', '\\ddotseq', '\\mbfzeta', '\\ltquest', '\\mbfscrb', '\\pushout', '\\supdsub', '\\nsubset', '\\neptune', '\\upomega', '\\mbfsans', '\\upsampi', '\\vzigzag', '\\Lbrbrak', '\\mbfscre', '\\ngtrsim', '\\alphaup', '\\nearrow', '\\succneq', '\\shuffle', '\\nwarrow', '\\simplus', '\\mitzeta', '\\nsucceq', '\\hzigzag', '\\mbffrak', '\\Coloneq', '\\thetaup', '\\dotplus', '\\project', '\\Upsilon', '\\Nwarrow', '\\rftimes', '\\eqqplus', '\\simless', '\\nvinfty', '\\Bbbfive', '\\upkappa', '\\frownie', '\\questeq', '\\Nearrow', '\\because', '\\precsim', '\\implies', '\\Bbbzero', '\\lsqhook', '\\partial', '\\plussim', '\\precneq', '\\mbfscrp', '\\Diamond', '\\subrarr', '\\twocups', '\\mbfbeta', '\\lessdot', '\\rrangle', '\\fbowtie', '\\cirscir', '\\mbfiota', '\\upalpha', '\\mbfscrc', '\\eqqless', '\\thermod', '\\succeqq', '\\mbfscrw', '\\jupiter', '\\Neptune', '\\Jupiter', '\\deltaup', '\\mbfscrv', '\\lftimes', '\\gtrless', '\\olcross', '\\mbfscrj', '\\lllnest', '\\coloneq', '\\veeodot', '\\leadsto', '\\mbfscrh', '\\between', '\\ddagger', '\\gtquest', '\\varclub', '\\mbfscrr', '\\scorpio', '\\suphsol', '\\squoval', '\\sigmaup', '\\obslash', '\\mbfscrg', '\\boxplus', '\\smallni', '\\annuity', '\\overbar', '\\napprox', '\\notowns', '\\mbfitmu', '\\varpiup', '\\mbfscri', '\\Bbbfour', '\\mbfitpi', '\\warning', '\\mbfscro', '\\sptilde', '\\greater', '\\maltese', '\\Searrow', '\\mbfscrf', '\\mbfscrk', '\\llcurly', '\\mathcal', '\\nsupset', '\\swarrow', '\\natural', '\\varsdef', '\\closure', '\\bumpeqq', '\\Uparrow', '\\mbfscrt', '\\submult', '\\gggnest', '\\mbfscra', '\\twocaps', '\\dbkarow', '\\updelta', '\\lessgtr', '\\benzenr', '\\mbfscrm', '\\backsim', '\\mbfscru', '\\llangle', '\\suplarr', '\\supedot', '\\mbfscrq', '\\mbfscrz', '\\varstar', '\\lozenge', '\\Mercury', '\\fatsemi', '\\revnmid', '\\yinyang', '\\mttfive', '\\pluseqq', '\\mttzero', '\\diceiii', '\\mercury', '\\trprime', '\\subedot', '\\mapsup', '\\fourth', '\\mbfitm', '\\ltrivb', '\\origof', '\\inttop', '\\dotsim', '\\mbfith', '\\mfrakg', '\\ltimes', '\\iotaup', '\\apprge', '\\msanst', '\\msansh', '\\subset', '\\msansn', '\\mfrakc', '\\taurus', '\\mbfitz', '\\mfrakt', '\\sumint', '\\mapsto', '\\preceq', '\\mbfitd', '\\supsim', '\\sqrint', '\\msanse', '\\eqless', '\\gtrdot', '\\isinvb', '\\second', '\\APLlog', '\\stareq', '\\Lambda', '\\succeq', '\\subsup', '\\veedot', '\\Square', '\\stigma', '\\mbfitq', '\\mbfitx', '\\supset', '\\Rbrack', '\\elsdot', '\\varphi', '\\mfrakp', '\\APLinv', '\\bigvee', '\\anchor', '\\mitvar', '\\wedgeq', '\\dprime', '\\mfrakm', '\\mbfitr', '\\barcap', '\\mitpsi', '\\capdot', '\\mttone', '\\lfloor', '\\bigbot', '\\mbfito', '\\msansk', '\\cupdot', '\\mbfite', '\\rtimes', '\\ltlarr', '\\msansq', '\\mitrho', '\\btimes', '\\Uranus', '\\msansf', '\\gemini', '\\mfrake', '\\msansx', '\\msanso', '\\mbfrho', '\\lparen', '\\varrho', '\\models', '\\mbfitk', '\\oslash', '\\boxast', '\\bigcup', '\\mfrakj', '\\msansu', '\\sslash', '\\lambda', '\\mathrm', '\\Supset', '\\msansd', '\\hslash', '\\gesdot', '\\gtrarr', '\\mfraka', '\\Bbbsix', '\\mbfitc', '\\cancer', '\\mbfitn', '\\barcup', '\\mbfitb', '\\mfrako', '\\msansj', '\\msansa', '\\mathbb', '\\nvdash', '\\simgtr', '\\mfraks', '\\intcup', '\\laplac', '\\eqqsim', '\\iiiint', '\\msansp', '\\mfrakv', '\\egsdot', '\\supsub', '\\cirbot', '\\bigcap', '\\mbfitw', '\\danger', '\\oiiint', '\\tminus', '\\mfrakd', '\\iinfin', '\\pisces', '\\mbfchi', '\\mbfits', '\\subsub', '\\candra', '\\eqcirc', '\\eparsl', '\\mfrakz', '\\mathtt', '\\qprime', '\\msansm', '\\msanss', '\\angdnr', '\\mfrakf', '\\eqeqeq', '\\barvee', '\\CIRCLE', '\\iddots', '\\invnot', '\\diceiv', '\\Bbbsum', '\\intbar', '\\vbrtri', '\\mbfpsi', '\\betaup', '\\dagger', '\\mbfitp', '\\bigtop', '\\pounds', '\\upzeta', '\\invneg', '\\mfrakw', '\\zetaup', '\\intcap', '\\Bbbone', '\\boxbar', '\\spddot', '\\forall', '\\bowtie', '\\mfrakx', '\\mbfity', '\\MapsUp', '\\rbrace', '\\rfloor', '\\upbeta', '\\exclam', '\\lgroup', '\\rbrack', '\\veebar', '\\nsimeq', '\\mfraky', '\\mathit', '\\msansz', '\\saturn', '\\midcir', '\\mtttwo', '\\mfrakb', '\\circeq', '\\bullet', '\\coprod', '\\mbfitg', '\\assert', '\\mbfita', '\\apprle', '\\Bbbtwo', '\\Mapsto', '\\nunlhd', '\\smiley', '\\mfrakn', '\\angles', '\\mbfphi', '\\nasymp', '\\Circle', '\\square', '\\mbfitu', '\\msansl', '\\niobar', '\\pencil', '\\varnis', '\\mbfiti', '\\Stigma', '\\Taurus', '\\mfrakh', '\\lowint', '\\bumpeq', '\\mbfvar', '\\uminus', '\\lbrace', '\\scurel', '\\msansv', '\\rgroup', '\\ominus', '\\parsim', '\\prurel', '\\mfrakq', '\\msansg', '\\lbrack', '\\daleth', '\\supsup', '\\mbfitl', '\\mfrakl', '\\mitphi', '\\neuter', '\\uranus', '\\Gemini', '\\mbfitj', '\\gtlpar', '\\exists', '\\msansr', '\\topcir', '\\period', '\\mbfitf', '\\rparen', '\\Rparen', '\\msansc', '\\mitchi', '\\Subset', '\\mfrakr', '\\Otimes', '\\utilde', '\\propto', '\\otimes', '\\ovhook', '\\invamp', '\\mfraku', '\\approx', '\\nequiv', '\\mbfscr', '\\diceii', '\\mbfitv', '\\gesles', '\\mathbf', '\\subsim', '\\boxbox', '\\Lbrack', '\\mfraki', '\\upiota', '\\lesdot', '\\ddddot', '\\Vvdash', '\\nunrhd', '\\mbftau', '\\mathsf', '\\gtrsim', '\\swords', '\\lesges', '\\mbfeta', '\\atsign', '\\rangle', '\\dicevi', '\\msansb', '\\miteta', '\\sumtop', '\\topbot', '\\measeq', '\\Exclam', '\\mbfitt', '\\boxdot', '\\mittau', '\\msansy', '\\Lparen', '\\Bumpeq', '\\female', '\\cupvee', '\\eqqgtr', '\\droang', '\\mathds', '\\mfrakk', '\\msansi', '\\msansw', '\\Saturn', '\\mttsix', '\\cirmid', '\\langle', '\\mitnu', '\\cdotp', '\\Vdash', '\\oplus', '\\perps', '\\mbfpi', '\\hfill', '\\mbfxi', '\\vdots', '\\uplus', '\\uptau', '\\tplus', '\\Colon', '\\Sampi', '\\chiup', '\\skull', '\\Sqcap', '\\imath', '\\lsime', '\\breve', '\\operp', '\\upvar', '\\smile', '\\csupe', '\\sqint', '\\ularc', '\\virgo', '\\Venus', '\\upphi', '\\times', '\\mscrt', '\\nrres', '\\isins', '\\mscrx', '\\delta', '\\Omega', '\\adots', '\\Qoppa', '\\eqdot', '\\slash', '\\ndres', '\\Micro', '\\psurj', '\\sqcup', '\\mbfnu', '\\BbbPi', '\\libra', '\\lrarc', '\\check', '\\zpipe', '\\unrhd', '\\mscrr', '\\Equiv', '\\lceil', '\\mscrg', '\\house', '\\omega', '\\rhoup', '\\upint', '\\mscru', '\\upold', '\\mscrm', '\\zhide', '\\mscrj', '\\Libra', '\\gtcir', '\\tauup', '\\fltns', '\\cdots', '\\uprho', '\\alpha', '\\wedge', '\\mscrw', '\\Bbbpi', '\\qoppa', '\\mscrf', '\\jmath', '\\mbfit', '\\lnsim', '\\upeta', '\\pluto', '\\dddot', '\\kappa', '\\upchi', '\\varpi', '\\nsucc', '\\iiint', '\\forkv', '\\tcohm', '\\mscrs', '\\Theta', '\\mscrn', '\\arceq', '\\phiup', '\\mscri', '\\sqcap', '\\mscra', '\\eqdef', '\\Vvert', '\\sigma', '\\sampi', '\\mfrak', '\\mscrk', '\\psiup', '\\earth', '\\csube', '\\Equal', '\\theta', '\\oiint', '\\Sqcup', '\\awint', '\\Dashv', '\\unlhd', '\\sphat', '\\llarc', '\\lblot', '\\asymp', '\\nless', '\\doteq', '\\gsiml', '\\mscrv', '\\minus', '\\amalg', '\\Wedge', '\\Doteq', '\\DashV', '\\mscrb', '\\dicei', '\\grave', '\\asteq', '\\simeq', '\\mscre', '\\prime', '\\Gamma', '\\ldots', '\\mscrl', '\\equiv', '\\ncong', '\\VDash', '\\dashv', '\\Euler', '\\mscrp', '\\Koppa', '\\strns', '\\nabla', '\\mbfmu', '\\gimel', '\\sharp', '\\infty', '\\mitpi', '\\comma', '\\mscry', '\\ltcir', '\\tilde', '\\mitmu', '\\dicev', '\\xbsol', '\\uppsi', '\\Delta', '\\vdash', '\\gescc', '\\colon', '\\barin', '\\nhpar', '\\mscro', '\\lescc', '\\third', '\\veeeq', '\\upand', '\\DDDot', '\\mscrd', '\\notni', '\\mscrh', '\\angle', '\\gamma', '\\msans', '\\nprec', '\\Pluto', '\\mscrz', '\\nsime', '\\gnsim', '\\eqsim', '\\mscrq', '\\ocirc', '\\frown', '\\gneqq', '\\eqgtr', '\\forks', '\\lsimg', '\\Sigma', '\\notin', '\\lneqq', '\\equal', '\\Aries', '\\aleph', '\\etaup', '\\ddots', '\\rblot', '\\acute', '\\mitxi', '\\koppa', '\\rceil', '\\gsime', '\\aries', '\\urarc', '\\disin', '\\mscrc', '\\mttm', '\\fint', '\\dlsh', '\\eqeq', '\\mbfb', '\\lang', '\\leqq', '\\upxi', '\\Bbbl', '\\mbfn', '\\mitq', '\\mitr', '\\iint', '\\mbfu', '\\csup', '\\mitj', '\\mbfl', '\\geqq', '\\mttn', '\\Bbbw', '\\Bbbp', '\\piup', '\\mbfh', '\\Bbbc', '\\siml', '\\Bbbu', '\\mtty', '\\XBox', '\\sdef', '\\Bbbt', '\\BbbS', '\\tcmu', '\\Bbbk', '\\BbbO', '\\mitx', '\\Bbbz', '\\csub', '\\mbfq', '\\Game', '\\dres', '\\tosa', '\\circ', '\\Mars', '\\psur', '\\BbbU', '\\mitk', '\\xiup', '\\hash', '\\upmu', '\\rsub', '\\mttg', '\\mttx', '\\hide', '\\mitu', '\\semi', '\\intx', '\\rbag', '\\BbbG', '\\nisd', '\\nmid', '\\isin', '\\mbfi', '\\Bbbs', '\\mbfk', '\\mbfc', '\\plus', '\\mitm', '\\lnot', '\\flat', '\\tinj', '\\beta', '\\ring', '\\mbfv', '\\Rdsh', '\\gets', '\\Bbbh', '\\mtta', '\\BbbJ', '\\gtcc', '\\nuup', '\\BbbM', '\\mbfd', '\\mitn', '\\tsur', '\\BbbA', '\\prod', '\\Bbbv', '\\mbfj', '\\mits', '\\BbbT', '\\pinj', '\\mttj', '\\Ldsh', '\\Bbbn', '\\mite', '\\beth', '\\DDot', '\\obot', '\\ddot', '\\mita', '\\buni', '\\ffun', '\\mitp', '\\male', '\\zcmp', '\\mitg', '\\BbbW', '\\mitd', '\\Bbbd', '\\simg', '\\BbbI', '\\cong', '\\BbbP', '\\lneq', '\\lbag', '\\mbfx', '\\mttb', '\\Bbbj', '\\girl', '\\mbfs', '\\land', '\\Bbbb', '\\star', '\\mbff', '\\miti', '\\dint', '\\Bbby', '\\rimg', '\\quad', '\\BbbB', '\\BbbY', '\\mitl', '\\mito', '\\mitw', '\\limg', '\\mttp', '\\BbbQ', '\\sans', '\\Prec', '\\spot', '\\mttf', '\\BbbN', '\\rang', '\\BbbK', '\\mbfy', '\\upin', '\\pfun', '\\vert', '\\Bbbx', '\\Vbar', '\\mbfm', '\\BbbH', '\\mttz', '\\xsol', '\\mbfe', '\\mbfa', '\\mbfg', '\\VERT', '\\mbfz', '\\uppi', '\\BbbE', '\\mitf', '\\odiv', '\\lvec', '\\odot', '\\mity', '\\smte', '\\ltcc', '\\nleq', '\\Rbag', '\\mbfp', '\\zeta', '\\Bbbe', '\\prec', '\\mttk', '\\mttu', '\\sqrt', '\\tona', '\\BbbX', '\\duni', '\\dash', '\\owns', '\\Lbag', '\\Bbbo', '\\less', '\\nexi', '\\mitc', '\\fcmp', '\\cent', '\\Finv', '\\succ', '\\mttd', '\\iota', '\\dsub', '\\Bbbg', '\\surj', '\\Vert', '\\Bbbf', '\\BbbF', '\\mbfo', '\\Bbbm', '\\mttt', '\\Bbbq', '\\mitv', '\\Same', '\\Bbbr', '\\finj', '\\BbbR', '\\mbfr', '\\mitz', '\\ngeq', '\\mttl', '\\mtti', '\\cdot', '\\mlcp', '\\Perp', '\\mttw', '\\euro', '\\BbbV', '\\ngtr', '\\BbbC', '\\upnu', '\\Barv', '\\BbbZ', '\\mbfw', '\\mttr', '\\comp', '\\mtts', '\\Zbar', '\\Bbbi', '\\muup', '\\Join', '\\mttq', '\\LVec', '\\gneq', '\\rres', '\\mtte', '\\mtth', '\\obar', '\\dsol', '\\BbbD', '\\perp', '\\towa', '\\late', '\\tfun', '\\Bbba', '\\mttv', '\\drsh', '\\mtto', '\\mitb', '\\oint', '\\mbft', '\\mitt', '\\mscr', '\\mttc', '\\BbbL', '\\nsim', '\\Succ', '\\toea', '\\Bot', '\\mbf', '\\cup', '\\Lsh', '\\cos', '\\Mho', '\\Phi', '\\fun', '\\Top', '\\vee', '\\lll', '\\yen', '\\nis', '\\leo', '\\dot', '\\geq', '\\boy', '\\max', '\\Vec', '\\log', '\\int', '\\rel', '\\div', '\\lor', '\\Rsh', '\\ggg', '\\Not', '\\cat', '\\rhd', '\\QED', '\\bar', '\\glj', '\\RHD', '\\eth', '\\mho', '\\psi', '\\rho', '\\mit', '\\Leo', '\\top', '\\lhd', '\\var', '\\tau', '\\leq', '\\mtt', '\\LHD', '\\not', '\\sin', '\\min', '\\mid', '\\neq', '\\neg', '\\sun', '\\sim', '\\Psi', '\\cap', '\\Yup', '\\gla', '\\phi', '\\iff', '\\exi', '\\sum', '\\tan', '\\cir', '\\chi', '\\inj', '\\nni', '\\ell', '\\ast', '\\bij', '\\Sun', '\\vec', '\\smt', '\\Vee', '\\bot', '\\Cup', '\\Cap', '\\Dot', '\\eta', '\\lat', '\\nin', '\\hat']
import re
def latex_Standardize(ltx):
"""
latex格式清洗规范化
:return:
"""
ltx = ltx.replace(":", ":").replace(",", ",").replace("。", ".").replace(";", ";").replace("?", "?") \
.replace("!", "!").replace(".", ".").replace("、", "、").replace("∶", ":").replace("…", "...") \
.replace(")", ")").replace("(", "(").replace("·", " \cdot ").replace("′", "'").replace("α", "\\alpha")
LATEX_SYMS.sort(key=lambda i: len(i), reverse=True)
sub2ltx = {}
num = 1
for syb in LATEX_SYMS:
if syb in ltx:
ltx = ltx.replace(syb, "【{}】".format(num))
sub2ltx["【{}】".format(num)] = syb + " " # 加空格
num += 1
if "\\" in ltx:
continue
else:
break
for k1, v1 in sub2ltx.items():
ltx = ltx.replace(k1, v1).replace(" ", " ")
return ltx
# aa=r"{\sqrt{5gR-\dfrac{5EqR}{m}}\leqv0<\sqrt{6gR-\frac{5EqR}{m}}}"
# tt=latex_Standardize(aa)
# print(int(80/1.27+1))
ltx2url = {'1': ' ', '{A\\cdot (-\\infty ,\\frac{1}{2}\\rbrack }': '
', '{A\\cdot (-\\infty ,\\frac{1}{2}\\rbrack }': ' ', '{(-\\infty ,\\frac{1}{2})}': '
', '{(-\\infty ,\\frac{1}{2})}': ' ', '{y=bx+a}': '
', '{y=bx+a}': ' ', '{X\\sim B(20,\\frac{1}{2}),}': '
', '{X\\sim B(20,\\frac{1}{2}),}': ' ', '{R^{2}}': '
', '{R^{2}}': '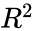 ', '{AC_{1}\\perp }': '
', '{AC_{1}\\perp }': '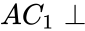 ', '{B_{1}CD_{1}}': '
', '{B_{1}CD_{1}}': '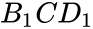 ', '{2\\sqrt {2}}': '
', '{2\\sqrt {2}}': ' ', '{B_{1}D_{1}}': '
', '{B_{1}D_{1}}': '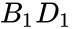 '}
def sub2(s):
if s:
all_ltx = re.findall(r'\$.*?\$', s) # 查找试题结构中的公式
all_ltx.extend(re.findall('\\\\\(.*?\\\\\)', s))
all_ltx = list(set(all_ltx))
for ltx in all_ltx:
new_ltx = ltx.replace("$", "").replace("\\(", "").replace("\\)", "")
if new_ltx in ltx2url: # 将latex换为其渲染图片的线上可访问地址
s = s.replace(ltx, ltx2url[new_ltx])
return s
one_items = {"options_img": [
"
'}
def sub2(s):
if s:
all_ltx = re.findall(r'\$.*?\$', s) # 查找试题结构中的公式
all_ltx.extend(re.findall('\\\\\(.*?\\\\\)', s))
all_ltx = list(set(all_ltx))
for ltx in all_ltx:
new_ltx = ltx.replace("$", "").replace("\\(", "").replace("\\)", "")
if new_ltx in ltx2url: # 将latex换为其渲染图片的线上可访问地址
s = s.replace(ltx, ltx2url[new_ltx])
return s
one_items = {"options_img": [
" $1$",
"
$1$",
" ",
"
",
" ",
"
",
" "
],}
# k = "options_img"
# if k == "options_img":
# one_items[k] = list(map(sub2, one_items[k]))
# print(one_items)
# items_str = "
"
],}
# k = "options_img"
# if k == "options_img":
# one_items[k] = list(map(sub2, one_items[k]))
# print(one_items)
# items_str = " |t0b>|br\s*/?>'
r'|/?(p|span|font|article|ul|ol|div|table|t?body|html|head|t[drh])(\s*|\s+style=.*?")>'
r'|/?[a-z]+ style=.*?">)', ss.group(1)) is None:
print(ss.group(1))
return "<{}".format(ss.group(1))
else:
return "<{}".format(ss.group(1))
aabb = """
|t0b>|br\s*/?>'
r'|/?(p|span|font|article|ul|ol|div|table|t?body|html|head|t[drh])(\s*|\s+style=.*?")>'
r'|/?[a-z]+ style=.*?">)', ss.group(1)) is None:
print(ss.group(1))
return "<{}".format(ss.group(1))
else:
return "<{}".format(ss.group(1))
aabb = """
2020-2021年福州高级中学高二上期末考试试卷
\n\n
物理试卷答案
\n一、选择题
二、实验题
\n21.【答案】0.772 ×1 12
22.【答案】如图 V1 R1 0.11
""" # html2txt = re.sub("<([^<]{1,30})", sub2, aabb) # print(html2txt) # import hashlib # name_list = random.sample(range(100000, 999999), 1) # word_id_temp = str(int(time.time())) + str(name_list[0]) # print(word_id_temp) # md = hashlib.md5() # md.update(word_id_temp.encode("utf-8")) # word_id = str(md.hexdigest()) # print(word_id) # html2txt = """ # 6.超声波测速是一种常用的测速手段。如图所示,安装有超声波发射和接收装置的测速仪B # 固定在道路某处,A为测速仪B正前方的一辆小汽车,两者相距为338m。某时刻B发出超 # 声波,同时A由静止开始做匀加速直线运动。当B接收到反射回来的超声波信号时,A、B相 # 距为346m,已知声速为340m/s,则下列说法正确的是 # A.A车加速度的大小为${2m//s^{2}}$ #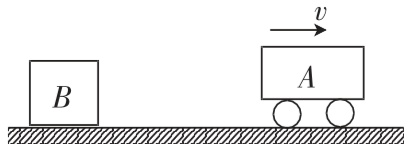 # B.超声波追上A车时,A车前进了4m
# C.经过2s,测速仪B接收到返回的超声波
# D.测速仪B接收到返回的超声波时,A车的速度为16m/s
# """
# html2txt = re.sub('w\s*w\s*w\..*?(\.\s*c\s*o\s*m|\.cn)+|(?(\d+)\.', str(svg_html_data))]
# topicidx = [i[0] for i in topicinfo]
# topicno = [i[1] for i in topicinfo]
# print(topicidx)
# time3 = time.time()
# all_mathjax1 = [[a.start(), a.group(1)] for a in
# re.finditer('(()*)', str(svg_html_data))]
# print("all_mathjax1:", len(all_mathjax1), all_mathjax1)
# for n, jax in enumerate(all_mathjax1):
# svgs = re.findall("
# B.超声波追上A车时,A车前进了4m
# C.经过2s,测速仪B接收到返回的超声波
# D.测速仪B接收到返回的超声波时,A车的速度为16m/s
# """
# html2txt = re.sub('w\s*w\s*w\..*?(\.\s*c\s*o\s*m|\.cn)+|(?(\d+)\.', str(svg_html_data))]
# topicidx = [i[0] for i in topicinfo]
# topicno = [i[1] for i in topicinfo]
# print(topicidx)
# time3 = time.time()
# all_mathjax1 = [[a.start(), a.group(1)] for a in
# re.finditer('(()*)', str(svg_html_data))]
# print("all_mathjax1:", len(all_mathjax1), all_mathjax1)
# for n, jax in enumerate(all_mathjax1):
# svgs = re.findall("